CopyCat - A Simple Intro to User Input and Variables via Scratch

My child and I worked on CopyCat as a simple introduction to variables and user input in Scratch. Algebra is part of the Grade 4 Math curriculum in the USA, and this project could be a fun way to introduce the use of variables.

Aim:  

Design an interactive game in Scratch, where a CopyCat copies/repeats everything that you type in.

The Design Process:

• Only a single sprite is required: the CopyCat. You can either choose from the list of sprites already available on Scratch, or draw your own. 

• To provide user interaction in starting and stopping the game, we used the "green flag click" to start and the "space key click" to stop the game (both of which can be found under the section "Events" in the Scripts area in Scratch). You can choose any of the options that are available in "Events" to do the same.

Various sections in the Scripts area of Scratch

And now the fun part: CopyCat needs to copy everything that you type in.
How can we achieve this?

• Under "Sensing" in the Scripts area in Scratch, you will find a block that asks for user input and waits for it. This is what we shall use, to ask the user to type in anything they like.

• Once the user input is received, CopyCat needs to repeat it. But, how can CopyCat remember what the user typed in? Here is where the concept of variables comes into play. In the section "Sensing", you will find the variable "answer", which stores whatever the user typed in. 

• I recommend selecting the box right next to "answer", so that it is visible on the screen and the kids can see how its value varies (hence the name variable), depending on the user input.

• The CopyCat can now use this variable along with the "say" instruction (found in the "Looks" area of Scripts in Scratch), to repeat/copy whatever the user types in.

Ask the students to try writing the code upto this point:

1. When "green flag clicked" (or other event), CopyCat asks the user to type in something.
2. CopyCat repeats the user input, via the variable "answer". 
3. When "space key clicked" (or other event), stop the program.

Let the students experiment with different values for the user input and observe how the variable changes accordingly. Once comfortable with the use of the variable, they can hide it by deselecting the box next to "answer".  It would be good to remind the students at this point, that this feature is helpful for debugging.

Here are three screen shots to demonstrate how the user input gets stored in the variable "answer".

  Asking for user input; variable is empty

User input entered; variable is empty till Return key is pressed

User input is now stored in the variable

Nets of 3D Shapes Part 2 - Prisms & Pyramids: More Practice with Procedures using Pro-Bot

This programming assignment is intended to provide more practice with Procedures using Pro-Bot. We shall use Procedures to store programs for various polygons. We shall then write programs for Pro-Bot to draw nets of some 3-Dimensional figures using these Procedures. 

We already worked on the nets of cubes in our previous assignment,  Nets of 3D Shapes Part 1 - Cubes. This is a follow-up to that work, involving more complex polyhedrons. 

Computer Science concepts involved:   Sequential programming, Repeat loops, Procedures

Math concepts involved:   Polyhedrons (prisms, pyramids), Nets of 3D figures (visualizing 3D figures on a 2D plane, identifying multiple nets, properties of nets), Polygons (triangles, quadrilaterals, pentagons), Measurement, Angles

Material required:  Card paper/thin cardboard to draw the nets on

Extension activity:   Make the 3D figures by cutting out the net from the card paper and folding along the edges 

Grade levels:   5

Hours required:   2 or more

Nets of 3-Dimensional Figures

A 3-Dimensional (3D) shape is a shape that has length, width and depth. They are also called solid figures or solid shapes. The length, width and depth are the three dimensions. Most of the objects that we see around us are 3-Dimensional. For example: your books, school bag, a box of crayons, Pro-Bot, table, chairs, water bottle, soccer ball, even yourselves are all 3D shapes.

How do these shapes differ from 2-Dimensional (2D)  figures, like the ones that you draw on paper? Think about how a cube or a sphere differs from a square or a circle drawn on paper. Well, the difference is that they have depth, unlike the 2D figures drawn on paper, which have only length and width. 3D shapes do not lie flat on a plane surface and they are difficult to draw on a piece of paper. 

But what if we could open up the 3D shapes and lay them out flat on paper? This would show us exactly how these solid shapes are made. A net can help us convert a 3D shape to a 2D figure. Nets are the flattened shapes of 3D objects. The net shows every edge and every face of the 3D figures laid out flat on paper. The net has only length and width; it does not have depth. It makes it easier for us to study and analyze some of the properties of a 3D object. You can cut out the net from the paper and fold it along the edges to create the 3D object. The same 3D object may be flattened into more than one net.

Let’s look at a few 3D shapes and draw their nets. We shall use Pro-Bot to draw the nets on thin cardboard. You can then cut out the nets and fold them to create the 3D shapes.

Nets of Prisms:

A prism is a solid object whose bases (or ends) have the same size and shape and are parallel to each other. The sides of the prism are parallelograms. A prism has the same cross-section all along its length. The shape of the bases (or ends) give the prism its name. We shall look at two types of prisms here:

• Rectangular prisms
• Triangular prisms

Nets of Rectangular Prisms:

Rectangular prisms are very commonly seen in our daily lives; for example, boxes, books, buildings, etc. A rectangular prism has 6 rectangular faces, 12 edges and 8 vertices. Opposite faces are congruent and have the same dimensions.  All faces of the rectangular prism are rectangles. A cube is a rectangular prism where all rectangular faces have equal edges.

Given below is a rectangular prism and one of its nets. The bases of this prism are square in shape. Hence it is also called a square prism. 

1. Write a program for Pro-Bot to draw the net given in the figure. Store the program for each rectangular face as a Procedure. (If there is a procedure for the 6 cm side square that you have already written, it can be used in this program as well.) 
2. Can you come up with more nets for the above prism. Try at least one other net and write a program for Pro-Bot to draw it. 
3. Once you are done drawing each net using the Pro-Bot, cut out the net from the paper. You can fold the paper along the edges and create the prism.
4. Given below is another rectangular prism. Write a program for Pro-Bot to draw a net for this prism. 

  

Nets of a Triangular Prism:

In the figure below, you can see a triangular prism, with a shape that resembles a camping tent. It has 5 faces, two of which are equilateral triangles and three are rectangles. 

1. Write a program for Pro-Bot to draw an equilateral triangle of sides 6 cm and store it as a Procedure on Pro-Bot. Remember to use Repeat Loops when you are working with regular polygons (polygons with all edges equal and all angles equal).
2. Next, construct a net for this triangular prism. Write a program for Pro-Bot to draw the net, using the Procedures for the rectangle and the triangle that you previously wrote.
3. How many different nets can you draw for this triangular prism? Write a program for Pro-Bot to draw each net that you can identify for this prism.

Nets of Pyramids:

The word “pyramid” immediately brings to mind the royal tombs of ancient Egypt. The pyramids of Egypt are square pyramids, with a square base and triangular sides. There are various types of pyramids; they are named according to the shape of the base. A pyramid is made by connecting the base to the apex (top point where all the triangular sides meet). 

In this assignment we shall look at three regular pyramids, which have regular polygons as their base: 

• Triangular Pyramid
• Square Pyramid
• Pentagonal Pyramid

Net of a Triangular Pyramid/Tetrahedron:

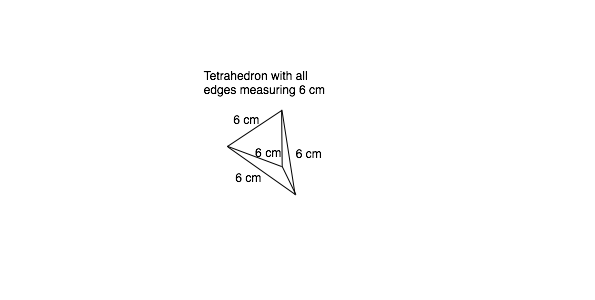
A triangular pyramid is also known as a tetrahedron ("having 4 faces"). A tetrahedron has 4 triangular faces, 4 vertices and 6 edges. Three triangular faces meet at each vertex. 

In the figure below, a tetrahedron with 6 cm edges is given. All the triangular faces are equilateral triangles, with sides of 6 cm. 

1. Can you write a program for Pro-Bot to draw a net for the tetrahedron, using the Procedure for the equilateral triangle of sides 6 cm that you wrote earlier? 
2. How many nets can you create for the tetrahedron?
3. After drawing the net using Pro-Bot, you can cut the net out of the paper and fold it along the edges to build the 3D tetrahedron. 

Net of a Square Pyramid:

A square pyramid has 5 faces, 5 vertices and 8 edges. The base is a square and the other faces are triangles. In the figure below, a square pyramid with all edges measuring 6 cm is given. 

1. Can you write a program for Pro-Bot to draw a net for this pyramid, using some of the Procedures that you wrote earlier? 
2. How many nets can you create for the square pyramid?
3. After drawing the net using Pro-Bot, you can cut the net out of the paper and fold it along the edges to build the pyramid. 

Net of a Pentagonal Pyramid:

A pentagonal pyramid has 6 faces, 6 vertices and 10 edges. The base is a pentagon and the other faces are triangles. In the figure below, a pentagonal pyramid with all edges measuring 6 cm is given. 

1. Can you write a program for Pro-Bot to draw a net for this pyramid, using some of the Procedures that you wrote earlier? Remember to use Repeat Loops while writing the program for the pentagon. 
2. How many nets can you create for this pyramid?
3. After drawing the net using Pro-Bot, you can cut the net out of the paper and fold it along the edges to build the pyramid. 

Solutions: Modular Programming with Squares on Pro-Bot

This is a subset of solutions for the assignment Modular Programming with Squares. This is just one way of coding the solutions, there are multiple correct solutions for the same.

Breaking Down Squares

1.  The shape is a square. It can drawn using the code:

Rpt 4 [    
Fd 12
Rt
]

2.  The above square needs to be divided into two equal parts. You can do this with a horizontal or vertical line across the middle or divide the square along the diagonal. The solution below divides the cake along the horizontal line
across the middle.

Rpt 4 [
Fd 12
Rt
]
Fd 6
Rt
Fd 12

3.  The square now needs to be divided into quarters. Two possible solutions, along the diagonals or using horizontal & vertical lines. The solution below divides the cake along the horizontal & vertical lines.

Rpt 4 [
Fd 12
Rt
]
Fd 6
Rt
Fd 12
Bk 6
Lt
Fd 6
Bk 12

4.  Here is another way to divide the cake into quarters, along the diagonals.

Rpt 4 [
Fd 12
Rt
]
Rt 45
Fd 17
Lt 135
Fd 12
Lt 45
Bk 17

5.  You need to divide the 12 x 12 cake into 9 equal pieces in this case.  Each slice is going to be 4cm x 4 cm.  Here is a solution using Nested Loops.

Rpt 4 [
Fd 12
Rt
]
Rpt 2 [
Rpt 2 [
Fd 4
Rt
Fd 12
Bk 12
Lt
]
Fd 4
Rt
]

Building Up with Squares as the Basic Building Blocks

1.  The square can be drawn using the code:

Rpt 4 [
Fd 6
Rt
]

2.   Here is the code for the rectangle drawn without using Nested Loops:

Rpt 4 [

Fd 6
Rt
]
Fd 6
Rpt 4 [
Fd 6
Rt
]
Fd 6
Rpt 4 [
Fd 6
Rt
]

3.  As seen from the code above, there is a repeating pattern. After drawing each square, you need to move to the starting position for the next square. The above code can be rewritten using Nested Loops as:

Rpt 3 [
Rpt 4 [
Fd 6
Rt
]
Fd 6
]

4. & 5.  To draw the large square that is double the size of the small square, different techniques can be employed. The easiest is to start from the midpoint of the figure. Each time, draw the small square and then turn 90 degrees to the right. Here is the code that uses Nested Loops.

Rpt 4 [
Rpt 4 [
Fd 6
Rt
]
Rt
]

Solutions to the Hopscotch figure:

Rpt 3 [      // Start drawing the rectangular part of the hopscotch from bottom left corner
Rpt 4 [
Fd 6
Rt
]
Fd 6
]
Rt             // Here, you want to try and get to the midpoint of the large square
Fd 3         // 3 cm from the top of the rectangle to the midpoint of large square
Lt
Fd 6         // You have reached the midpoint of the large square now
Rpt 4 [     // Now draw the large square using the previously written code for the same
Rpt 4 [
Fd 6
Rt
]
Rt
]

Breaking Down & Building Up: Modular Programming with Squares on Pro-Bot

We have already worked on drawing squares using Pro-Bot. We used Repeat Loops to create a square in our previous assignment here

Now, let’s work a bit more with squares, first breaking it down into smaller parts and then building up compound figures using squares as our basic building blocks.

Computer Science concepts involved:   Sequential programming, Repeat loops, Nested Loops, Modular programming

Math concepts involved:   Polygons (squares, rectangles), Measurement, Fractions, Compound figures, Angles

Grade levels:   3, 4, 5

Hours required:   2 or more

Breaking Down Squares

1.   You have spent your Sunday afternoon at home baking a delicious chocolate cake. You baked the cake in a square pan that measures 12 cm long on each side. What shape is your cake when you look at it from above? Can you draw this shape using Pro-Bot? 

2.   You plan to share the cake with 2 of your friends. You cut the cake into equal parts for yourself and your friends. Using Pro-Bot can you draw a figure to represent your cake and how you would cut it? What fraction of the cake would each person get? 

3.   One more friend comes along. So, you decide to cut the cake into equal parts for yourself and your 3 friends. Using Pro-Bot can you draw a figure to represent your cake and how you would cut it? What fraction of the cake would each person get now? 

4.   How many different ways can you think of to cut the cake into 4 equal parts? Using Pro-Bot, draw figures to represent each case. What shapes are the fractions in each case? 

5.   Your friend says that a single serving of cake should be no larger than 4 cm x 4 cm in size. How would you cut the cake to get slices of this size? Using Pro-Bot, draw a figure to represent your cake and how you would cut it in this case.  How many pieces can you cut the cake into?

Building Up with Squares as the Basic Building Blocks

1.   Use Pro-Bot to draw a square of sides 6 cm each. (Remember to use Repeat Loops for drawing the square).

2.   Now, let’s create a rectangular shape with the following dimensions, using the above 6 cm square as our building block:  

Length  =  3 x length of one side of the square 

Width  =  length of one side of the square 

Can you write a program for Pro-Bot to draw this figure, using the program for the 6 cm side square that you wrote earlier? 

  

3.   Can we use Nested Loops to draw the above figure? Explain why.

4.   Next, let’s create a bigger square with the following dimensions:       

Side of big square  =  2 x Side of the 6 cm square

Can you write a program for Pro-Bot to draw this figure, using the program for the 6 cm side square that you wrote earlier? 

5.   Can we use Nested Loops to draw the above figure? (Tip: It is easier to start drawing from the midpoint of the figure while using Nested Loops.)

Here is a set of possible solutions to the above assignments.

Modular Programming

From the two examples above, you can see how a small module that performs one distinct function (in this case, our program to draw the 6 cm side square) can be used to build bigger components. The big components that we created in turn can work as modules for an even bigger program. 

This activity provides a quick peek into modular programming, a principle that is widely used in most programming languages. Modular programming is the process of dividing a program into smaller, separate sub-programs. 

Let's look at an example that is familiar to you. Do you play with Lego construction sets? A lot of times, when you buy Lego sets, the box comes with several small bags inside of it, each labeled with a number. There will be an instruction booklet that tells you how to use the tiny pieces inside each bag to create a small component of the big toy that you plan to make. Once you have created a couple of such components from the different bags, the book tells you how to put them together to create a slightly bigger unit... and the process goes on till you get to the completed product... 

Just like you build large Lego toys using multiple smaller units, each of which in turn was made of still smaller pieces, we can build large programs using smaller components or modules, which in turn can be made of even smaller modules.

So, why do we prefer to use modular programming rather than develop one giant program? Here are some reasons...

• Reusing the code. You write a module just once, but it can be used multiple times by different programs. In the above examples, you wrote the code for the 6 cm side square just once, but you used it multiple times while developing two different programs. 
• Breaking up the program into smaller modules makes it easier to maintain the program. For example, if you decide to change the larger programs to be using 10 cm side squares, all you need to do is make one change in your smallest module for the square from 6 cm to 10 cm. The change is easily reflected in all the bigger modules that use it. 
• It is easier to find and fix errors in smaller modules. 
• Smaller modules ensure that the code is short, simple, easy to read and understand.
• It makes it easier for different people to develop different modules independent of each other. You could have one person write the program for the 6 cm square, another person write the program for the rectangle using the 6 cm square and yet another person write the program for the bigger square. And then, all of these could be put together to create an even bigger program as seen below...

1.   Elmo and his friends are planning to play hopscotch. Elmo suggests a figure that looks like the following and draws it out using Pro-Bot. Each square in this hopscotch figure has 6 cm sides. Can you write a program for Pro-Bot to draw this figure? Can you re-use the programs that you wrote above to draw this figure?

• You can also store each of the programs that you wrote above (for the rectangle and the big square) as separate Procedures and call them from your Main program for Pro-Bot to draw the hopscotch figure.

A Different Approach to the above Program

If you have an even number of students/ groups working on this project, you could try the following exercise with the hopscotch figure:

• Divide the class into an even number of teams, so that each team pairs with another.  Let’s call the teams in each pair as Team A & Team B.
• Team A in each pair would create the procedure for the big square. Team B in each pair would create the procedure for the large rectangle.
• The pairs then exchange the Pro-Bots.
• So now, each team has the procedure that they created themselves plus the procedure that was created by the other team. They do not need to know how the other team created their procedure;  they just need to know what it does (a black box).
• Each team shall give clear instructions to their partner team as to how their procedures work. They can even draw a picture to show what their procedure would create, specifying the start & end points, and give it to the other team.
• Each team now integrates the procedures/modules (their own work + the other team’s work) to create the required final result & test it.
• This could be a good activity to introduce the kids to the concepts of real world engineering projects: division of work among different teams, testing & integration of results.

Applying Fractions to Polygons

In this programming assignment, we shall draw polygons and divide them into fractions using Pro-Bot. This assignment can be a follow-up to the one where we learned to draw various polygons using Pro-Bot. We shall use sequential programming for drawing irregular polygons and Repeat Loops to draw regular polygons. Next, we shall divide the polygons into specified fractions using Pro-Bot as our drawing tool.

Computer Science concepts involved:   Sequential programming, Repeat loops

Math concepts involved:   Polygons (regular and irregular), Linear & Angular Measurements, Fractions, Area, Congruence

Grade levels:   3, 4, 5

Hours required:   2 or more

Polygons

In geometry, a polygon refers to a closed, two-dimensional figure formed by a set of straight line segments. The straight line segments are called the polygon’s edges or sides, and the points where two edges meet are the polygon's vertices or corners.

If all edges are equal and all angles are equal, then it is a regular polygon. Else, it is an irregular polygon.

Square:

1. Use Pro-Bot to draw a square of sides 8 cm. Each interior angle is 90 degrees.
2. Divide the square horizontally into quarters (1/4) using Pro-Bot as your drawing tool. 
3. Divide the square vertically into quarters (1/4) using Pro-Bot as your drawing tool.
4. Divide the square into 4 equal squares, using Pro-Bot as your drawing tool. What fraction of the large square does each small square occupy?
5. Divide the square into 2 equal sized triangles, using Pro-Bot as your drawing tool. Are the triangles congruent? 

Rectangle:

1. Use Pro-Bot to draw a rectangle of sides 4 cm and 6 cm. Each interior angle is 90 degrees.
2. Divide the rectangle into thirds along the longer side using Pro-Bot as your drawing tool. 
3. Divide the rectangle into halves along the shorter side using Pro-Bot as your drawing tool.
4. Divide the rectangle into quarters using Pro-Bot as your drawing tool.
5. Divide the rectangle into 2 triangles along a diagonal, using Pro-Bot as your drawing tool. Are the triangles congruent? Are they equal in area?

Rhombus:

1. Use Pro-Bot to draw a rhombus of sides 6 cm. One pair of opposite interior angles is 60 degrees each and the other pair is 120 degrees each. 
2. Divide the rhombus into thirds, using Pro-Bot as your drawing tool.
3. Divide the rhombus into sixths (1/6) using Pro-Bot as your drawing tool. Are the fractions congruent shapes? Are they rhombuses? If not, what shapes are they?

Parallelogram:

1. Use Pro-Bot to draw a parallelogram of sides 4 cm and 6 cm. One pair of interior opposite angles is 45 degrees each and the other pair is 135 degrees each (Remember that for a parallelogram, opposite angles are equal).
2. Divide the parallelogram into 2 equal parallelograms, using Pro-Bot as your drawing tool. What fraction of the original parallelogram is occupied by the smaller ones?
3. Considering that the minimum dimension that can be provided by Pro-Bot is 1 cm, what is the maximum number of smaller parallelograms that you can divide up the larger parallelogram into, using Pro-Bot as your drawing tool? What fraction of the larger parallelogram is occupied by each of the smaller units?

Equilateral Triangle:

1. Use Pro-Bot to draw an equilateral triangle of sides 6 cm. Each interior angle is 60 degrees.
2. Divide the triangle into 2 equal triangles, using Pro-Bot as your drawing tool.
3. Divide the triangle into 3 triangles of equal area, using Pro-Bot as your drawing tool. You can do this in a couple of ways: 

• Divide one side of the triangle into 3 equal parts. Then draw lines connecting the opposite vertex to the two points that trisect the side. 
• Find the centroid: If you draw a line from each vertex to the midpoint of the opposite side, the point at which all three lines meet is the centroid. Draw a line from each vertex to the centroid to divide up the triangle into 3 equal triangles.

Solutions: Drawing Polygons using Pro-Bot

Here is a subset of the possible solutions for drawing the polygons in this assignment. Please keep in mind that there are multiple correct ways of programming each of these figures.


The following programs draw the polygons without using Repeat Loops.

1. Square of sides 8 cm:

Fd 8
Rt
Fd 8
Rt
Fd 8
Rt
Fd 8

2. Rectangle 4 cm x 6 cm: 

Fd 4
Rt
Fd 6
Rt
Fd 4
Rt
Fd 6

3. Parallelogram 4 cm x 6 cm:

Fd 4
Rt 45
Fd 6
Rt 135
Fd 4
Rt 65
Fd 6

4. Rhombus 6 cm:

Fd 6
Rt 60
Fd 6
Rt 120
Fd 6
Rt 60
Fd 6

5. Equilateral Triangle of sides 6 cm:

Fd 6
Rt 120
Fd 6
Rt 120
Fd 6 

6. Right Triangle of sides 3 cm, 4 cm, 5 cm:

Fd 3
Rt 126
Fd 5
Rt 144
Fd 4 

Drawing Regular Polygons using Repeat Loops in Pro-Bot

All of the regular polygons below have sides of 6 cm.

1. Equilateral Triangle

Rpt 3 [
Fd 6
Rt 120
]

2.  Square

Rpt 4 [
Fd 6
Rt 90
] 

// You can also use the instruction "Rt", instead of "Rt 90" in the code above,                                           // as the default turn is 90 degrees for Pro-Bot.

3. Pentagon

Rpt 5 [
Fd 6
Rt 72
]

4. Hexagon

Rpt 6 [
Fd 6
Rt 60
]

5. Octagon

Rpt 8 [
Fd 6
Rt 45
]

6. Nonagon

Rpt 9 [
Fd 6
Rt 40
] 

7. Decagon

Rpt 10 [
Fd 6
Rt 36
]

A Circle using a Repeat Loop

Rpt 360 [
Fd 1                 // Move 1 cm
Rt 1                 // Turn 1 degree
]

An Algorithm for Drawing Regular Polygons using Repeat Loops 

From the pieces of code above for various regular polygons, the relation between the number of sides of a regular polygon and the angle of turn can be deduced to 360/N where N is the number of sides of the polygon.

The generalized algorithm for drawing regular polygons is:

Rpt N [
Fd X
Rt 360/N
]

where N is the number of sides of the regular polygon, X is the length of each side of the polygon.  

Drawing Polygons using Pro-Bot

In this programming assignment, we shall draw polygons using Pro-Bot. We shall start by using sequential programming to draw the polygons. Next, we shall look at some regular polygons and learn how to use Pro-Bot’s Repeat Loops to draw them. We shall also develop a generalized algorithm to draw regular polygons using Pro-Bot. We can store programs for the polygons as Procedures on Pro-Bot.

Computer Science concepts involved:  Sequential programming, Repeat loops, Algorithm development

Math concepts involved:  Polygons (regular and irregular), Linear & Angular Measurements, Interior angles, Supplementary angles

Grade levels:  3, 4, 5

Hours required:  3 or more

Polygons

In geometry, a polygon refers to a closed, two-dimensional figure formed by a set of straight line segments. The straight line segments are called the polygon’s edges or sides, and the points where two edges meet are the polygon's vertices or corners.

We see polygons of different types all around us in our daily lives. Here is an interesting article that I found on mathforum.org, as to where we see different types of polygons in our daily lives.

If all edges are equal and all angles are equal, then it is a regular polygon. Else, it is an irregular polygon.

Square:

Use Pro-Bot to draw a square of sides 8 cm. Each interior angle is 90 degrees.

Rectangle:

Use Pro-Bot to draw a rectangle of sides 4 cm and 6 cm. Each interior angle is 90 degrees.

Parallelogram:

Use Pro-Bot to draw a parallelogram of sides 4 cm and 6 cm. One pair of interior opposite angles is 45 degrees each and the other pair is 135 degrees each.

Note: Remember that for a parallelogram, opposite angles are equal. 

In the figure of the parallelogram above, angles marked ‘a’ are equal; they are opposite angles. Similarly, angles marked ‘b’ are equal; they too are opposite angles. The angles ‘a’ and ‘b’ add up to 180 degrees; ‘a’ and ‘b’ are supplementary angles.

Note: Remember that when Pro-Bot has to draw a 45 degree interior vertex, it would have to turn 135 degrees and not 45 degrees, assuming it was moving in the forward direction before making the turn. Similarly for the 135 degree vertex, Pro-Bot would have to turn 45 degrees. Can you see why?

Rhombus:

Use Pro-Bot to draw a rhombus of sides 6 cm. One pair of opposite interior angles is 60 degrees each and the other pair is 120 degrees each. 

Next, use Pro-Bot to draw a rhombus of sides 6 cm. One pair of opposite interior angles is 90 degrees each. What shape do you get?

Equilateral Triangle:

Use Pro-Bot to draw an equilateral triangle of sides 6 cm. Each interior angle is 60 degrees.

Note: Remember that when you draw an equilateral triangle using Pro-Bot, at each vertex Pro-Bot has to turn 120 degrees (supplementary angle), and not 60 degrees, assuming it was moving in the forward direction before making the turn. Can you see why?

Right Triangle:

Use Pro-Bot to draw a right triangle of sides 3 cm, 4 cm and 5 cm. The interior angle between the 4 cm and 5 cm sides is 36 degrees. The interior angle between the 3 cm and 5 cm sides is 54 degrees. The interior angle between the 3 cm and 4 cm sides is 90 degrees.

Note: Remember that when you draw a right triangle using Pro-Bot, at each vertex Pro-Bot has to turn at its supplementary angle, and not the interior angle, assuming it was moving in the forward direction before making the turn. 

Drawing Regular Polygons using Repeat Loops in Pro-Bot

For the various shapes above that you drew using ProBot, you could see that in the case of programs for for the regular polygons (polygons with equal sides and equal interior angles), there is a pattern of instructions that keeps repeating multiple times. 

You can rewrite your programs for the square and the equilateral triangle using Repeat Loops in Pro-Bot. 

Use Pro-Bot to draw each of the shapes below. Use Repeat Loops to write your programs.

1. Equilateral Triangle:   Use Pro-Bot to draw an equilateral triangle of sides 6 cm. Each interior angle is 60 degrees.
2. Square:    Use Pro-Bot to draw a square of sides 6 cm. Each interior angle is 90 degrees.
3. Pentagon:   Use Pro-Bot to draw a pentagon of sides 6 cm. Each interior angle is 108 degrees.
4. Hexagon:    Use Pro-Bot to draw a hexagon of sides 6 cm. Each interior angle is 120 degrees.
5. Octagon:    Use Pro-Bot to draw a octagon of sides 6 cm. Each interior angle is 135 degrees.
6. Nonagon:   Use Pro-Bot to draw a nonagon of sides 6 cm. Each interior angle is 140 degrees.
7. Decagon:   Use Pro-Bot to draw a decagon of sides 6 cm. Each interior angle is 144 degrees.

After drawing the various polygons, ask the students to identify a few examples of where they might see these shapes in their daily lives. For example: a sandwich cut in half is a triangle, roof trusses are triangles, a STOP sign is an octagon, a YIELD sign is a triangle, cells in beehives/ honeycombs are hexagons, etc.

Here is a set of solutions for this assignment.

Develop an Algorithm for drawing Regular Polygons using Pro-Bot

Now that you have written programs for Pro-Bot to draw various regular polygons, let us develop a generalized algorithm for the same.

1. Is it more efficient to use Repeat Loops or Sequential Programming when you write programs for regular polygons on Pro-Bot?
2. From your programs above, can you identify a technique to find the angle at which Pro-Bot should turn at each vertex for a regular polygon?
3. Given the length of a side of a regular polygon and the angle you found using your above technique, can you write a program for drawing a regular polygon of N sides (N being any whole number) using Pro-Bot?
4. Can you now generalize your method and write down the various steps involved, as an algorithm.

Experiment more with Regular Polygons using Pro-Bot:

1. While developing your algorithm, did you notice that as the number of sides of the polygon increases, the shape of the polygon tends to a circle? What happens to the interior angle of the polygon in this case; does it increase or decrease?
2. What happens to the angle at which Pro-Bot has to turn as the number of sides of the polygon increases? Does it increase or decrease?
3. What is the smallest measurement of angle that you can use on Pro-Bot? What is the smallest length that you can draw using Pro-Bot?
4. Using the algorithm that you developed above for Pro-Bot, draw a regular polygon using that uses the smallest angle and the smallest length that Pro-Bot can provide as its dimensions. What shape do you get? 
5. Draw a regular polygon using Pro-Bot, just like the one in the previous question, that uses the smallest degree of angle, but with the length of the side increased by 1 unit. What shape do you get? 
6. What happens to the shape if you keep increasing the length of the side by 1 unit at a time, but keep the angle constant at the smallest value?
7. What happens if you increase both the length and the angle by 1 unit each time? What difference do you see?

Challenge Question: 

1. Can you write a program for Pro-Bot to draw a circular maze (a spiral shape) using all of the ideas that you learned from the above questions? It is easier to start the spiral from inside and start moving outwards. Start the spiral with the smallest length and angle that Pro-Bot can provide and then build outwards.